| (1) |
Пока она свежая в ней могут быть ошибки и опечатки, в том числе в формулах, но за конечный результат я ручаюсь.
В этой статье будет рассмотрена тема суммы бесконечных рядов вроде:
И так далее...
При этом одни скажут что сумма этих рядов равна бесконечности и
обсуждать здесь нечего, другие, более продвинутые в вопросе, вспомнят дзета
функцию Римана, скажут что
![]() ,
,
![]() ,
,
![]() и тоже добавят, что
обсуждать здесь нечего. Но что если я скажу, что здесь не всё чисто?
Что если я скажу что значение суммы этих рядов зависит... От чего она зависит
чуть позже.
и тоже добавят, что
обсуждать здесь нечего. Но что если я скажу, что здесь не всё чисто?
Что если я скажу что значение суммы этих рядов зависит... От чего она зависит
чуть позже.
Итак возьмём к примеру первый ряд два раза, но второй раз сдвинем его на один элемент:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | ... | ||
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | ... |
Вычтем второй ряд из первого и в результате получим:
| 1 | + | 0 | + | 0 | + | 0 | + | 0 | + | 0 | + | ... | = | 1 |
Если сдвинуть второй ряд на два элемента то аналогично разница будет 2, на три – 3 и т.д. Но как же так? Дзета функция Римана не предполагает подобных результатов и согласно ей результат будет равен строго нулю.
Но мы рассмотрим этот парадокс ближе и выведем, что таким
образом сумма (1) зависит от сдвига ![]() и если
обозначить значение при
и если
обозначить значение при ![]() как
как ![]() , то не
трудно вывести формулу для суммы (1) со сдвигом
, то не
трудно вывести формулу для суммы (1) со сдвигом ![]() :
:
Забегая вперёд заметим, что
![]() , потому что
скоро мы уже будем использовать это значение, но попутно
мы покажем откуда оно берётся.
, потому что
скоро мы уже будем использовать это значение, но попутно
мы покажем откуда оно берётся.
Во всяких доказательствах того что
![]() ,
активно используют ещё одну операцию помимо сдвига. Это разрядка:
,
активно используют ещё одну операцию помимо сдвига. Это разрядка:
| 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | 1 | + | ... | ||
| 2 | + | 2 | + | 2 | + | ... |
В первой строке разреженность ![]() равна
равна ![]() , во второй
, во второй ![]() ,
, ![]() .
Разница этих строк равна другому известному ряду:
.
Разница этих строк равна другому известному ряду:
| 1 | - | 1 | + | 1 | - | 1 | + | 1 | - | 1 | + | ... | = |
|
Сумму (1) с разреженностью ![]() и сдвигом
и сдвигом ![]() обозначим
обозначим
![]() и приведём пару её свойств:
и приведём пару её свойств:
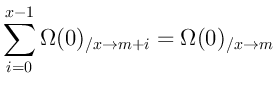
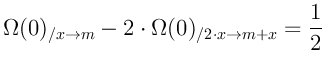
Этих двух свойств достаточно чтобы вывести формулу для разреженности
![]() :
:
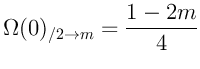
А если поиграться с другими значениями ![]() кратными двум, то зная
значения таких рядов как:
кратными двум, то зная
значения таких рядов как:
| 1 | - | 1 | - | 1 | + | 1 | + | ... |
| 1 | + | 1 | - | 1 | - | 1 | + | ... |
Легко вывести обобщённую формулу для суммы (1):
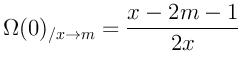
Но не будем останавливаться и перейдём к выводу формул для других степеней ряда:
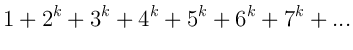
Которую мы обозначим как многие уже догадались за
![]() . А сумму
. А сумму ![]() её
членов за
её
членов за ![]() .
.
Сперва выведем формулу для ![]() (Если опущены, то
(Если опущены, то ![]() ,
, ![]() ).
).
Рассмотрим бесконечный треугольник:
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | . | ||||||||
| . | . | |||||||||
| . |
Суммируя его в трёх направлениях (по горизоантали, вертикали и диагонали) получим три суммы, которые равны между собой:
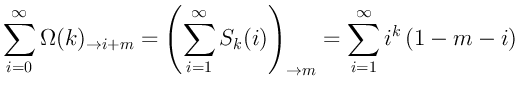
С первой формулой мы ничего делать не будем, а вот другие две возьмём
на вооружение и запишем чему они равны при ![]() :
:
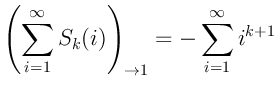
Раскроем обозначение ![]() и используем обозначение
и используем обозначение ![]() :
:
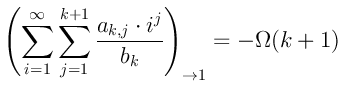
Вот из этой формулы следует, что при ![]()
![]() . Несмотря на что для её
вывода мы использовали сам этот факт, мы здесь просто не приходим к противоречию,
при других же значениях
. Несмотря на что для её
вывода мы использовали сам этот факт, мы здесь просто не приходим к противоречию,
при других же значениях ![]() будет противоречие.
будет противоречие.
Вынем ![]() -й член суммы слева из под знака суммы и поменяем местами знаки сумм
(от перемены мест слагаемых сумма не меняется):
-й член суммы слева из под знака суммы и поменяем местами знаки сумм
(от перемены мест слагаемых сумма не меняется):
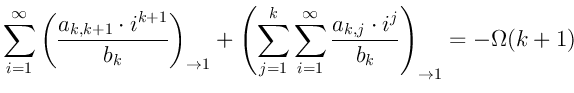
Обозначим бесконечные, суммы используя ![]() -нотацию:
-нотацию:
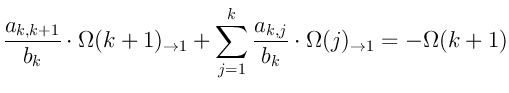
Умножим всё на
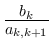 :
:
Далее отставим пока эту формулу и выведём ещё одну для
![]() ,
используя равенство:
,
используя равенство:
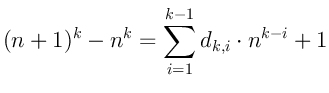
Получим:
Из (4) и (5) следует (мы использовали факт
![]() ):
):
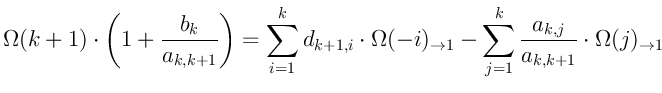
Ещё немного поколдуем и получим:
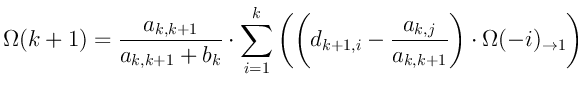
Пока нас интересует ![]() , которая из формулы очевидна равна нулю.
, которая из формулы очевидна равна нулю.
Введём ещё одну важную операцию над рядом ![]() . Пусть сумма состоящая из
каждого
. Пусть сумма состоящая из
каждого ![]() -го члена начиная с
-го члена начиная с ![]() -ого (
-ого (
![]() ) этого ряда
обозначается как
) этого ряда
обозначается как
![]() , например:
, например:
Можно показать что:
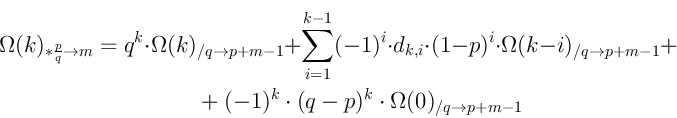
Используя это обозначение немного играя с разреженностью можно вывести:
Далее усовершенствуем немного формулу (5):
Формулы (6) и (7) используются совместно следующим образом.
В формуле (7) раскрываются суммы и все ![]() уже известных степеней,
далее осуществляется переход
уже известных степеней,
далее осуществляется переход
![]() . Далее заменяется
. Далее заменяется
![]() в формуле (6) только что полученным
значением при
в формуле (6) только что полученным
значением при ![]() . Из полученного равенства выводится формула для
. Из полученного равенства выводится формула для
![]() . Наконец это значение подставляется в формулу выведенную
из (7) и у нас готовая формула!
. Наконец это значение подставляется в формулу выведенную
из (7) и у нас готовая формула!
Я приведу здесь формулы для первых двух степеней:
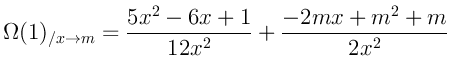
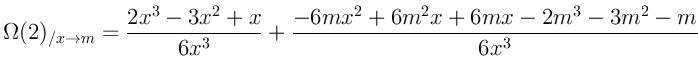
Можно заметить, что все формулы (за исключением нулевой степени) заметно
упрощаются при переходе ![]() :
:
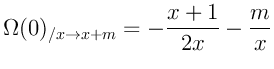
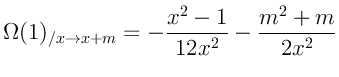
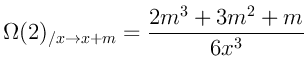
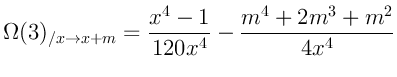
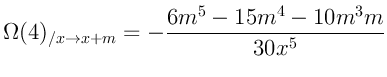
Когда есть пять формул на лицо становится очевидной их закономерность:
дело в том что в левой их части находится
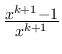 помноженное на значение Дзета-функции Римана, а в правой - формула суммы
первых
помноженное на значение Дзета-функции Римана, а в правой - формула суммы
первых ![]() членов ряда
членов ряда ![]() .
.
Немного поколдовав получим обобщённую формулу:
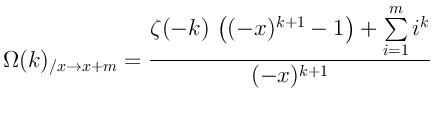
Эта формула не противоречит существующим данным о сумме некоторых бесконечных рядов:
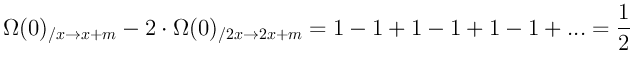
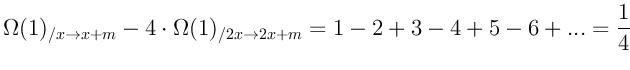
Не трудно заметить что при ![]() наша формула обращается в бесконечность. Таким образом те кто утверждает, что
сумма
наша формула обращается в бесконечность. Таким образом те кто утверждает, что
сумма ![]() рядов равна бесконечности правы, но сваливают всё в одну кучу, т.е. пытаются просуммировать
ряд с нулевой разреженностью. При
рядов равна бесконечности правы, но сваливают всё в одну кучу, т.е. пытаются просуммировать
ряд с нулевой разреженностью. При
![]() и
и ![]()
![]() -функция обращается в
-функция обращается в ![]() -функцию,
Таким образом те кто утвержадает что значение этих рядов совпадает с Дзета-функцией Римана тоже правы,
но разреженность в этом случае явлется мало того что отрицательной, так ещё и дробной, что делает такие
выводы совсем не интуитивными.
-функцию,
Таким образом те кто утвержадает что значение этих рядов совпадает с Дзета-функцией Римана тоже правы,
но разреженность в этом случае явлется мало того что отрицательной, так ещё и дробной, что делает такие
выводы совсем не интуитивными.
А теперь о том как интуитивно представить результаты полученные с помощью ![]() -функции.
Дело в том что я давно подозревал, что числовая ось - на самом деле кольцо. Это следует из предела:
-функции.
Дело в том что я давно подозревал, что числовая ось - на самом деле кольцо. Это следует из предела:
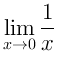
Продолжая эту мысль, представим, что происходит с рядом ![]() при движении за бесконечность.
Правильно! Оно превращается в минус бесконечность и уходит к нулю с отрицательными
значениями членов ряда:
при движении за бесконечность.
Правильно! Оно превращается в минус бесконечность и уходит к нулю с отрицательными
значениями членов ряда:
Сумма такой последовательности на кольце совершенно интуитивно равна нулю.
При смещении последовательности в право на единицу, мы выбрасываем крайнюю
![]() за ось, таким образом сумма ряда становится равной
за ось, таким образом сумма ряда становится равной ![]() .
При смещении ещё на единицу, "за борт" уходит
.
При смещении ещё на единицу, "за борт" уходит ![]() и сумма равна
и сумма равна ![]() .
И так далее. Всё это хорошо работает при нечётном
.
И так далее. Всё это хорошо работает при нечётном ![]() , при чётном в логике
появляется явный изъян: и на положительной и на отрицательной полуоси
значения положительные, а их сумма всё равно ноль.
Объяснить это я не могу, во всяком случае пока.
, при чётном в логике
появляется явный изъян: и на положительной и на отрицательной полуоси
значения положительные, а их сумма всё равно ноль.
Объяснить это я не могу, во всяком случае пока.
При разреженности ![]() оказывается что ряд на самом деле как бы
"расплывается" до ряда растущего с аналогичной скоростью, но без пробелов.
И "за борт" уходят значения именно этого ряда, а не начального.
оказывается что ряд на самом деле как бы
"расплывается" до ряда растущего с аналогичной скоростью, но без пробелов.
И "за борт" уходят значения именно этого ряда, а не начального.
Вот такие пироги, вот такие бесконечности...
Автор: Николай (unDEFER) Кривченков
Дата публикации: 24.11.2019
This document was generated using the LaTeX2HTML translator Version 2018 (Released Feb 1, 2018)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation formula.tex
The translation was initiated on 2019-11-24